1 言語の定義

1.1 目的
1.2 メカニズム
1.3 良い文法
1.4 文法のチェック
1.5 一般的な落とし穴
1.6 例
1.7 記述における注意
1.8 問題

コンパイラとは,ある言語で書かれたソース・プログラムを受け取り,アセンブリ言語やバイナリのマシン語などのオブジェクト言語で書かれた、ソース・プログラムと等価なオブジェクト・プログラムを出力するものである。すなわち、コンパイラとは入力のソース・プログラムを認識し、その文法と意味チェックを行ない、等価なオブジェクト・プログラムを作り出すものでなければならない。

コンパイラを作る前に、まず、言語の定義について考える必要がある。この章ではソース言語の文法を明らかにし、その文法の正当性を確かめる方法について述べる。次の章ではソース言語における個々の“単語”がどのように認識されるかを示す。第3章ではこれら二つがソース・プログラムを認識できるように組み合わされ、第4章では正しくないソース・プログラムに対しても適切な処置がなされるように拡張される。その後の章ではコンパイル時に必要な情報をどのように保ち、また、最終的なオブジェクト・プログラムを作り出すために、その情報をどのように用いるかについて述べる。

1.1 目的

言語の定義を構成する二つの要素は、シンタックスとセマンディックスである。シンタックスは,主に単語列あるいは文字列が言語上の“文”に相当するかどうかなど、言語の機械的な部分に関係する。そして文が何を意味するか(あるいは,文として正当であるか)は、言語のセマンディックスによって決定される。

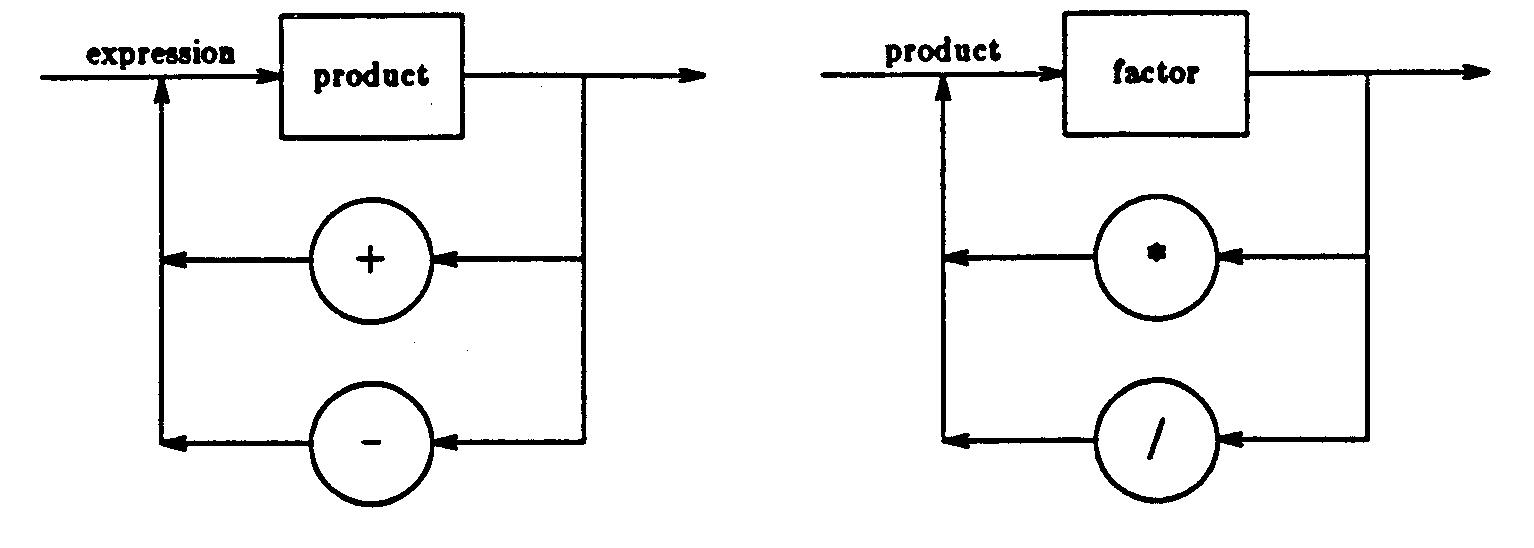
言語の正式な表記は、シンタックスとセマンディックスの両方の定義によって定められる。シンタックスは通常、“文の一部を記述するモデルの集まりである”ということができる。WirthがPascalを定義する時に初めて用いたシンタックス・グラフは,フローチャートのように書かれている。

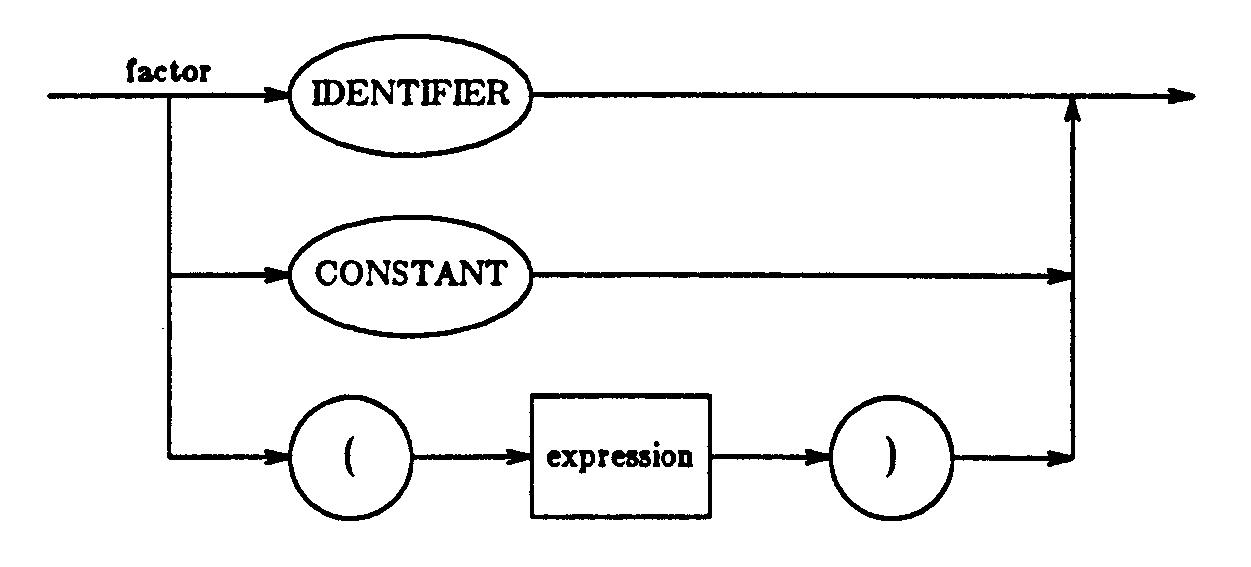
バッカス・ナウア・フォーム(Backus Naur Form,以下BNF)は、言語のシンタックス(BNF自身のシンタックスさえも)を示すことのできる一言語である。

expression
         : expression '+' product
	 | expression '-' product
	 | product

product
         : product '*' factor
	 | product '/' factor
	 | factor

factor
         : IDENTIFIER
	 | CONSTANT
	 | '(' expressoin ')'

BNFについては、後でさらに詳しく述べることにする。

言語のセマンディックスを記述することは、はるかに困難である。形式論に従うならば、良く定義された理論的なマシン・モデルで、あるいはその結果得られる仮想マシンの上で、文の実行をシミュレートする、文の意味の定義を行なう,また意味解釈のできない文を除外する、などを行なうことが必要である。

文あるいはその一部の意味を記述するために,普通の英語を使うこともできる。その場合、正式な表記法がないため、明確性と正確性が非常に重要となる。WirthのPascalやModula- 2の[Jen75]や[Wir82]の記述は非常に良い例となっているが、PL/IやFORTRAN言語のリファレンス・マニュアルは、破滅的といって良いほど冗長である。

シンタックスと、文に対して制限を与えるセマンディックスの記述は背反事項であると言える。BASICを例にとって考えてみよう。識別子identifierが次のように定義されていたとする。

id
        : LETTER DIGIT
	| LETTER
identifier
        : id '$'
	| id

もし、演算子十が数値の加算および文字列の結合に用いられるとすると、セマンディックスの記述は、十が文字列を数値に加えたり、あるいはその反対に用いられることができないようになっていなくてはならない。一方、次のように定義することもできる。

real_id
        : LETTER DIGIT
	| LETTER
string_id
        : real_id '$'

これにより、文字列と数値の計算を、言語の定義における純粋なシンタックスの意味において区別することができる。BASICの識別子の例は、シンタックスとするべきか、セマンディックスとするべきかの、ちょうど境界線にあると言える。一般的に言って、言語を定義する場合には、より正式な方法で定義されるべき英語などは用いないほうがよい。

1.2 メカニズム

BNFは言語のシンタックスを記述する形式である.これはPeter NaurがAlgo160の報告[Nau63]において用いたもので、以後多くの言語を記述するのに用いられている.現在では、BNFはさらに変更、拡張され、最終的な記述は容易には理解できないほどになっている[Wij75]。

言語のBNFによる記述として与えられる文法は、一連の規則からなる。そして規則は:で分けられた左辺と右辺がらなる。左辺は一つのユニークな非終端記号からなる。⁽²⁾右辺は1で区切られた一つ以上のフォーミュレーションからなる。それぞれのフォーミュレーションはO個以上の非終端または終端記号からなっている。規則にただ一つのフォーミュレーションしかない場合は、何もないのと同じことになる。1.1節で示した図の例を次に示す。

expression
         : expression '+' product
	 | expression '-' product
	 | product

product
         : product '*' factor
	 | product '/' factor
	 | factor

factor
         : IDENTIFIER
	 | CONSTANT
	 | '(' expressoin ')'

文法は,いかなる文が形作られるかを説明することにより,言語を定義するものである.第一の規則の左辺の非終端記号は開始記号となる.ここでは開始記号は式となっている.第一の規則には開始記号として可能なフォーミュレーションが挙げられている.それぞれのフォーミュレーションでは新たな非終端記号を導入している.この例ではproductがそれである.いかなる非終端記号にも規則がなければならない.そして,規則におけるどのフォーミュレーションも,他の非終端記号に置き換えることができる.置換えは,文法における開始記号から始めて,終端記号,すなわち一つの文となるまで繰り返される.終端記号は文法によってそれ以上説明されるものではない.それは単にその文法が記述している言語の文が書かれるアルファベットにすぎない.文法の規則が再帰的な形で非終端記号に入るとすれば,無限に長い文が可能となる.たとえば,前の例でフォーミュレーションに,expressionとしてproductを,productとしてfactorを,factorとしてIDENTIFIERを選ぶと,

 IDENTIFIER

がその例となる。他の例として、

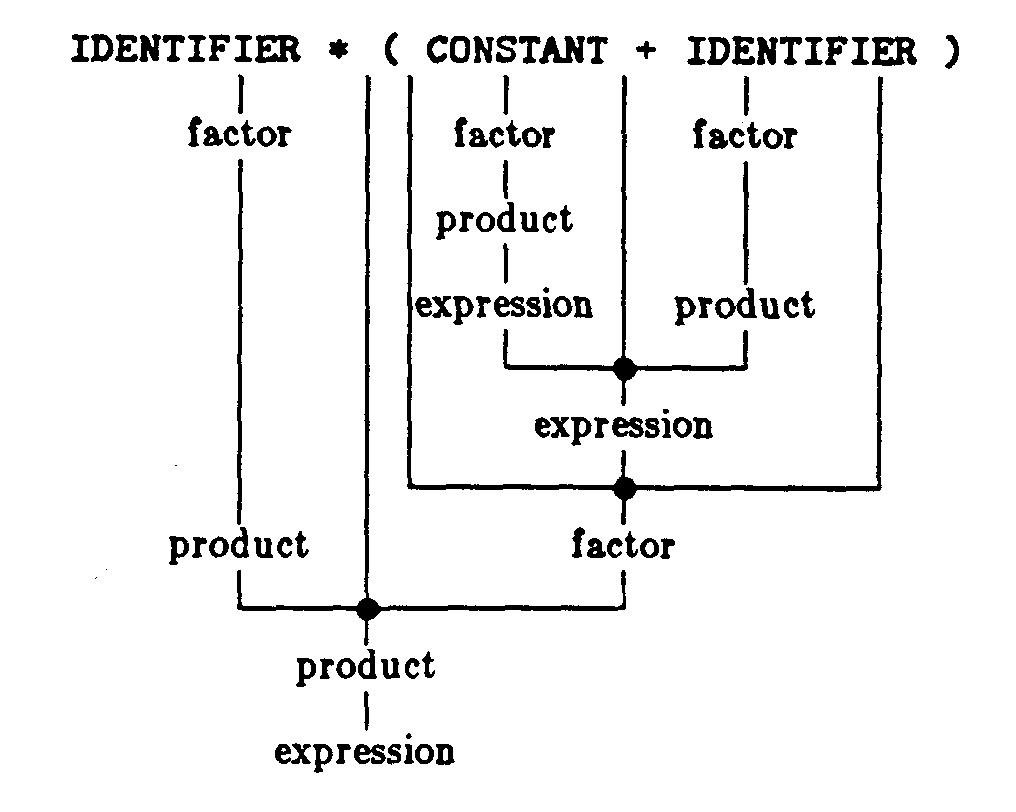
 IDENTIFIER * ( CONSTANT + IDENTIFIER )

が挙げられる。このような例では、“文法によって定義された文である”と結論するまでに、多くの中間のフォーミュレーションを使わねばならない。そこでそれらのフォーミュレーションを普通、パーズ・トリー(解析木)の形で表わす。この木の“根”には文法の開始記号の名前が与えられ、“葉”には文の終端記号の名前が与えられる。また、それぞれの非終端ノードには非終端記号の名前が与えられ、分岐点にはその非終端のフォーミュレーションの記号の名前が与えられる。

BNFはそれ自体が言語で、BNFによって記述することができる。

grammar
        : grammar rule
	| rule

rule
        : rule '|' formulation
	| NONTERMINAL ':' formulation
	| NONTERMINAL ':'

formulation
        : formulation symbol
	| symbol

symbol
        : NONTERMINAL
	| TERMINAL

この記述は、これまでに述べてきた非公式な定義に比べ、多少厳しいものとなっている。さて、ここでは空のフォーミュレーションが規則の最初になくてはならない。(なぜだろうか?)

例が示すように、再帰はBNFにおいて重要な役割を果たしている。規則は普通、左再帰で書かれる。つまり規則における非終端記号は、それ自身のフォーミュレーションの一つの初めにもう一度現われることになり、無限に長いシーケンスの元となる。このテクニックは、単純な事柄あるいは明快な言語のリファレンス・マニュアルを不明瞭にしてしまう傾向にある。そこで、任意の項目を囲む大カッコ([と])やO回以上現われる項目を囲む中カッコ({と})などの繰返しの構造を持つようにBNFが拡張された。場合によってはカッコを、優先順位を示すためや選択子である｜と記号の普通の結合を分けるために用いる場合もある。拡張BNFはBNFの記述に用いることも可能である。今後、次の記号の定義を変更する必要はほとんどないであろう。

symbol
        : NONTERMINAL
	| TERMINAL
	| '{' formulation '}'
	| '[' formulation ']'

算術式の文法も、次のように書き換えられる。

expression 
        : product { '+' product }
	| product { '-' product }
product
        : factor { '*' factor }
	| factor { '/' factor }

factorに関しては変更はない。

拡張BNF自身もまた、拡張BNFで記述することができる。

grammar
        : rule { rule }

rule
        : NONTERMINAL ':' [ formulation ] { '|' formulation }

formulation
        : symbol { symbol }

symbol
        : NONTERMINAL
	| TERMINAL
	| '{' formulation '}'
	| '[' formulation ']'

ここでの議論は正式のものではない。もちろん、用いた単語は適切なものである。非終端記号は、文字で始まり、文字と数字とアンダースコア(＿)からなる、プログラミング言語で言うところの識別子を意味している。終端記号は一般的に大文字で綴り、もし特殊文字1文字であれば引用符(')で囲む。ブランク文字(スペースとタブ)は普通意味を持たず、他の記号のデリミタとしてはほとんど用いない。

ここでは文脈自由言語について非公式にしか取り上げない。詳しく知りたい場合は[Aho77]を参照せよ。

1.3 良い文法

もし、言語を文の集合、すなわち一連の終端記号として定義するのなら、言語を記述する文法を定義する方法は数々ある。言語そのものは有限である必要はないが、言語の文法は有限であるべき定義によって表わされる。しかし、この制限だけでは十分でない。次の二つの簡単な算術式を記述する文法を考えてみる。

expression 
        : expression '-' IDENTIFIER
	| IDENTIFIER

expression
        : IDENTIFIER '-' expression
	| IDENTIFIER

どちらの文法にとっても、言語はIDENTIFIERと一が連続するものとなる。しかし、そこには重要な違いがある。一つの式の二つのパーズ・トリーを比較してみよう。

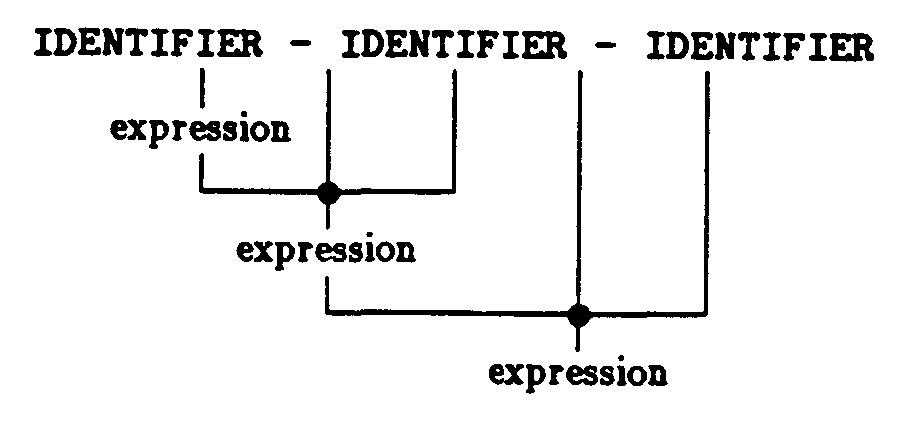
左再帰の文法は、左から始まる終端記号を見つけることになる。一方、右再帰の文法では、初めのパーズ・トリーをちょうど鏡に映した形(次の例)となる。

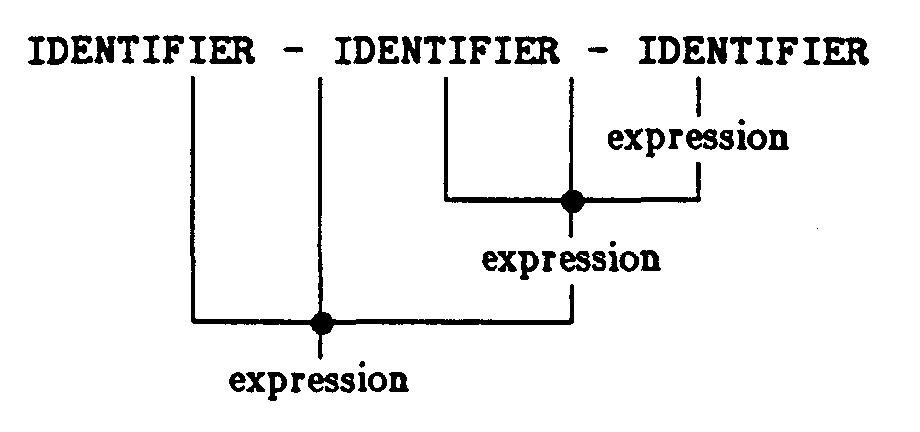
算術式の文においては、パーズ・トリーは、評価において結合される算術式の各項目の順番を定義する演算子の優先順位についても翻訳されなくてはならない。この例では、演算子は一つだけしか導入されていないので、優先順位の問題は生じない。しかし、文法によっては優先順位を導入するために、別の方法を用いなくてはならないであろう。左再帰文法では演算子に対して左から優先順位を付けることになり、右再帰の文法では右から優先順位が付けられることになる。ほとんどの演算子は左から評価されるのが普通であるため、左再帰が用いられるべきである。

しかし、問題はこれだけではない。同じ算術式の言語の文法のもう一つの記述を考えてみよう。

expression 
        : expression '-' expression
	| IDENTIFIER

この規則では、前に示した二つのパーズ・トリーの両方を生成することができる。したがって、この文法は曖昧な文法と呼ばれることになる。すなわち、二つの異なるパーズ・トリーが作られるような文が言語に存在することになる。曖昧さは文法によるものであって、言語が本来曖昧なわけではない。前の二つの例が示すように、この言語に曖昧さはない。つまり、必ず左から始まって、パーズ・トリーが作られるようにすることにより、明白にすることができる。これは、“明白化規則”として知られている。

コンパイラは第一の仕事として、翻訳されるべき言語を認識しなくてはならない。たとえば、終端記号の集まりとして認識し、そしてそれがその言語の文となるかどうかを判断しなくてはならない。問題はパーズ・トリーの生成にある。もし言語に明白な文法が与えられるなら、開始記号から始めて、順にフォーミュレーションを調べ、非終端記号に置き換え、文となるパーズ・トリーまでたどり着くことができる。しかし、このことはメカニズムとしてはバックトラックを行なうことを意味するだけで、それでは不十分である。さらに、もしコンパイラがパーズ・トリーを生成する時に出力を行なうならば、出力の一部を取り消すことがあるため、バックトラックでさえも困難になる。

言語認識のための良い文法は、明白であるばかりでなく、確実なものでなくてはならない。つまり入力に残りがある状態では、それに続く文となるべき終端記号は、部分的に生成されたパーズ・トリーとともにパーズ・トリーを完成させるための規則とフォーミュレーションを唯一決定できるか、あるいは、次の入力記号に合わせたパーズ・トリーを生成することができないことがわかるようになっていなければならない。

また、コンパイラ製作者の能力と用いるツールにも依存する問題であるが、文法の良さというものには別の面も存在する。たとえば、それぞれのフォーミュレーションが一つの終端記号から始まるように、十分単純にすることが挙げられる。このような場合では、次の入力記号だけで何がなされるべきかを決定されることになる。

最近のプログラミング言語の文法は、制限が少なくなる傾向にある。たとえば、普通はLL(1)やLR(1)などの機能を持つようになっている。LL(1)はバックトラックなしにトップダウンでパーズ・トリーを生成するもので、LR(1)はある種のテーブルとそのためのプログラムを用いて、バックトラックをせずにボトムアップでパーズ・トリーを生成するものである。どちらの場合も、いつでも次の入力記号を知るだけで良く、ただ一つの記号の先読みをするだけで良い。

LL(1)では、どの規則あるいはどのフォーミュレーションを使うべきかという問題が起こった場合に、次の入力記号が唯一すべきことを決定する。この問題は規則中のいくつかのフォーミュレーションから一つを選ばねばならない時に起こる。もし、どのフォーミュレーションも空でなければ、それは終端あるいは非終端記号のどちらかで始まることになる。そして次の入力記号はすべての(最初の)非終端記号のための、再帰も考えに入れたすべて選択可能なフォーミュレーションである終端記号のどれかとなり、フォーミュレーションの始まりにある終端記号にたどり着く。次の入力記号は必ずこれらの終端記号の一つでなければならず、したがってすべて異なるものとなる。もし空のフォーミュレーションであれば、次の状態となることのできる非終端記号のためのすべてのフォーミュレーションのもともとの終端記号を、さらに考慮に入れなければならない。

LL(1)を決定することは、“終端記号は非終端記号のためのフォーミュレーションで始まり、一つのフォーミュレーションにはそれぞれ二つの記号が統く”などのように表現できるため,実際それほど困難ではない。このような関係はプーリアンの行列[Gri71コで表わすことができる。あるいはより複雑な関係を用いて計算することも可能である。さらに,LL(1)を使うならば、言語の再帰的認識も非常に直接的なやり方で実現することが可能となる([Wir77]参照)。

たとえ文法が完全なLL(1)でなくとも、言語を認識し決定するためにある種のセマンディックスのための仕掛けを用いることができる。次のPascalのための記述の一部を考えてみよう。

statement
        : IDENTIFIER ':=' expression
	| IDENTIFIER

最初のフォーミュレーションは代入を示しており、次のものはプロシージャ・コールを示している。どちらのIDENTIFIERも等しく、その名前ではどのフォーミュレーションが使われるかを決定することはできない。この問題は,“プロシージャであるIDENTIFIERだけがプロシージャ・コールを始めることができ、そのようなIDENTIFIERでは代入を行なうことができない”、という認識によってごまかすことができる。Pascalにおいて名前は使われる前に宣言されなければならないため、このシンタックスの問題をセマンディックスの仕掛けによって解決することができる。

1.4 文法のチェック

コンパイラは、一連の終端記号がその言語の文となるかどうかを決定しなくてはならない。文法は言語の記述である。そこで、文法が認識の過程において多少なりとも使えるかどうか、という自然な疑問が生じる。

しかし第一に、文法はチェックされねばならない。したがって、すべての非終端記号のための規則が必要であり、すべての非終端記号は開始記号から到達可能でなければならない。文法は、認識に適するようにLL(1)のような性質を満足しなければならず、曖昧であってはならない。

Johnsonのyaccは、UNIXシステムの強力なユーティリティの一つで[Joh78]、上記の意味において文法のチェックを行なうために用いることができるものである。yaccほBNFで記述された文法を入力として、言語認識に適さない文法となるような点を指摘する。一例として、次の文法の記述ファイル(ファイル名grammar)を考えてみよう。

/*
 *     first example of a yacc grammar
 */

%token IDENTIFIER

%%

expression
        : expression '-' IDENTIFIER
	| IDENTIFIER

そして、次のコマンドによってテストを行なってみる。

yacc grammar

ここでは何も起こらないはずであり、また、起こってはならない。これはすなわち、この文法がyaccに適合したものであることを意味している。実際には、新しいファイルy.tab.cが作られるが、これについては第3章で詳しく述べる。

例で示されるように、yaccへの入力は前に述べたBNFの記述を用いている。終端記号は非終端記号と似ているため、ya?tでは終端記号は実際の文法の前に、%tokenを用いて定義しなければならない。また、%%の行が入力ファイルを二つに分けている。⁽³⁾ブランク等やC言語スタイルのコメントは無視される。

多少技術的なレベルで、yaCCがどのように文法をチェックするかを考えてみよう。([Bau76]の2.C章あるいは[Aho74]に,Homingがこの問題を計算機的な観点から解説している。)yaCCは文法をデバッグするための一つのオプションを持っている。次のようなコマンドを入力すると、

yacc -v grammar

以下に示すような内容の、y.outputというファイルが得られる。⁽⁴⁾

state 0
        $accept : _expression $end
	IDENTIFIER shift 2
	. error

	expression goto 1

state 1
        $accept : expression_$end
	expression : expression_- IDENTIFIER

	$end accept
	- shift 3
	. error

state 2
        expression : IDENTIFIER_   (2)

	. reduce 2

state 3
        expression : expression -_IDENTIFIER

	IDENTIFIER shift 4
	. error

state 4
        expression : expression - IDENTIFIER_   (1)

	. reduce 1

4/127 terminals, 1/175 nonterminals
3/350 grammar fules, 5/500 states
0 shift/reduce, 0 reduce/reduce conflicts reported
3/225 working sets used
memory: states,etc. 26/4500, parser 0/3500
3/400 disinct lookahead sets
0 extra closures
3 shift entries, 1 exceptions
1 goto entries
O entries saved by goto defau1t
Dptimizer space used: input 9/4500, output 4/3500
4 tab1e entries, O zero
maximum spread: 257, maximum offset: 257

ここではy.outputの内容をすべて示したが、それぞれの状態(state)の最初の2,3行だけが問題となる.y.outputの詳しい説門は3.1節で行なう。

yaCCは次の規則、

$accept: expression $end

を文法に加え、開始記号(この例ではexpression)の前にアンダースコア(＿)を用いて、規則中に位置マー力を付ける、これは状態state0と呼ばれる.次にya?tは,位置マー力を異なる開始記号に移そうとする。位置マー力が非終端記号の前に付けられた場合はいつでも、そのすべてのフォーミュレーションの前にも位置マーカが付けられる。一つの状態はこのように付けられた位置マーカ付きのフォーミュレーションの集まりとなる。位置マーカ付きのフォーミュレーションはコンブィグレーションと呼ばれる.

新しい状態は次のように求められる。古い状態のそれぞれのコンブィグレーションに対し、位置マー力が次の記号に移される。そして、同じ次の記号を持つすべてのコンブィグレーションに対してこれが繰り返される。このようにして、それぞれの可能な記号に対し,新しいコンブィグレーションが作られ、新しい状態となる。

前に述べたように、コンブィグレーション中の位置マーカが非終端記号の前に付けられた場合には,その記号のためのすべてのフォーミュレーションが,その始めに位置マー力を付けて状態に付け加えられなければならない。

この手続きには終りがなくてはならない。なぜなら、文法の定義において、規則,非終端記号、フォーミュレーションおよび終端記号は有限個であり、フォーミュレーションは有限の長さでなければならないからである。したがって、状態は有限となる。

この例では、state Oはyaccによって作られる。位置マーカは非終端記号であるexpressionに付いているため、すべてのフォーミュレーションに位置マー力を付けて加えなければならない。

expression : _expression - IDENTIFIER
expression : _IDENTIFIER

しかし、この部分はyaCCのアルゴリズムに照らし合わせれば明らかであるため、省略されている。このstateでは、位置マーカはexpressionとIDENTIFIERの前に付いている。これをすべてのコンブィグレーションのexpressionに移すことによりstate1が得られ、IDENTIFIERに移すことによりstate2が得られる。どちらのstateにも非終端記号の前の位置マー力がないので、新しいコンブィグレーションの結果は得られない。state2は位置マーカがフォーミュレーションの終りにたどり着く完全なコンブィグレーションだけを持つことになる。

state2では、位置マーカはyaccによって付け加えられた架空の$end記号と、他のコンブィグレーションにある終端記号の一に移すことができる。前者の操作は基本的には無視され、後者はstate3となる。

state3はもう拡張することができず、位置マーカはIDENTIFIERにのみ移され、state4にたどり着く。これでそのコンブィグレーションは終了したことになるため、これが最後の可能な状態となる。

もちろん、ここで述べたアルゴリズムは、入力の認識のための文法のすべての部分を使ったシミュレーションである。位置マーカを終端記号に移すこと、すなわちシフト(shift)は、入力におけるある位置の終端記号を受け入れることである。非終端記号に位置マー力を移すことは、その非終端記号のためのフォーミュレーションがシミュレーションのどこかで終了したことを意味する。(このことは第3章でさらに詳しく述べる。)

y.outputの各状態のコンブィグレーションの後のコメントは、それぞれの可能な入力記号を認識する時に、どのようなことが行なわれるかを示している。ピリオドは他のすべての記号を示しており、リデュース(reduce)は完成したコンブィグレーションが受け入れた記号の数を数えるため、あるいは適当な非終端記号によって置き換えられるために使われる可能性があることを示している。リデュースの後の数字は、使われるフォーミュレーションの数である。シフトは、それぞれの記号を受け入れるであろう次の状態を示している。

yaccに対する入力言語については、話の進行に従って徐々に説明していく。必要な場合には[Joh78]を参照せよ。
Linux, cygwinではy.outputの形式が若干異なり、error項は出力されず、状態を示す_も.に変わっている。

1.5 一般的な落とし穴

これまでの解析には何も悪いところはないように見えるが、実はそうではない。終端記号を定義するのを忘れたり、非終端記号のための規則を定義するのを忘れたり、開始記号からアクセス不可能な非終端記号や規則を加えたりすることは、明らかに誤りである。yaccはそれらを発見し、知らせてくれる。

文法における問題はそう単純ではなく、個々に注意が必要となる。次の普通のif文に関する記述の一部を考えてみよう。

/*
 *     dangling else
 */

%token IF...THEN
%token ELSE

%%
statement
        : ';'
	| IF...THEN statement
	| IF...THEN statement ELSE statement

yaccはシフトとリデュースが重複するという誤りを指摘するであろう。y.outputには次のように出力されているはずである。

4: shift/reduce conflict (shift 5, red'n 2) on ELSE
state 4
        statement : IF...THEN statement_    (2)
	statement : IF...THEN statement_ELSE statement

	ELSE shift 5
	. reduce 2

state 5
        statement : IF...THEN statement ELSE_statement

	IF...THEN shfit 3
	; shift 2
	. error

	statement goto 6

この問題は非常に一般的なもので、次のようなプログラムにおいて、e1seがどちらのifに属するものであるか、わからなくなることになる。

if (condition)
        if (condition)
	        ;                /* empty statement */
	else
	        ...

yaccではstate4において、終端記号ELSEを受け入れ(シフト)、二番目のコンブィグレーションに移るか、あるいは一番目のものを完成したコンブィグレーションと考え,非終端(リデュース)のステートメントに置き換えることのどちらもが可能である。シフトにおいて、elSeはもっとも内側のif文に対応付けられ、C言語やPasca1の要求に合致することになる。

すなわち、State4においてはシフトとリデュースは重複し、この例における文法はその誤りのため不明瞭で、言語認識に適さないものであることになる。しかし、yaCCでは意図しでそのような矛盾を許していて、非常に長い入力や、あえてそのように意図されたような場合に用いることができるようになっている。

次の問題はさらに深刻である。次の例はBASICで,その比較の結果が変数に代入されたり分岐に用いられる部分である。

/*
 *      multiple clauses
 */

%token IDENTIFIER, IF, THEN, SUM

%%

statement
        : IDENTIFIER '=' expression
	| IF condition THNE statement

condition
        : expression
	| SUM '<' SUM

expression
        : SUM '<' SUM
	| SUM

yaccは、リデュースとリデュースが重複していることを指摘するであろう。y.outputは次のようになる。

state 14
        condition : SUM < SUM_    (4)
	expression : SUM < SUM_    (5)

	. reduce 4

state14は二つ以上の完全なコンブィグレーションを持つ。このような場合、yaccは文法において最初に記述されたフォーミュレーションを用いるが、後で文法が変更された時に危険が生じる恐れがある。文法の作成に当たっては,普通,前述のelseの問題のようなシフトとリデュースの重複は容認するが、リデュースとリデュースの重複を引き起こすフォーミュレーションの組合せが存在する場合には、それを削除するように文法を書き換えるものである。この例ではそれは容易である。実際、この例はあまりに単純すぎて現実的でない。

/*
 *      multiple clauses, no conflicts
 */

%token IDENTIFIER, IF, THEN, SUM

%%

statement
        : IDENTIFIER '=' expression
	| IF expression THNE statement

expression
        : SUM '<' SUM
	| SUM

yaccは入力に対して非常に寛大である。これまで,規則の後のセミコロンを無視してきた。しかし,不用意に空のフォーミュレーションを加えると、驚くほどリデュースやシフトの重複が引き起こされるので、注意しなければならない。

もう一つの曖昧さは、実際、有効である。次の算術式のための文法を考えてみよう。

expression
        : expression '+' expression
	| expression '-' expression
	| expression '*' expression
	| expression '/' expression
	| IDENTIFIER

記述は短く、他の非終端記号はないが、演算子の優先順位等について他に何の記述も必要としない。優先順位等について、次のように入力フアイルの初めに明示しておく限り、yaccは前述のような記述を許す。

%token IDENTIFIER

%left  '+' '-'
%left  '*' '/'

%%

%leftは左優先で、同じ優先順位を持つ終端記号を定義するものである。優先順位は、入力ファイルにおいて%left、%right、%nonassocが出てくる順に高くなる。%rightは名優先で、%nonaSSoCは同じ優先順位を持ち、それら同士を組み合わすことができない終端記号である。

これらの曖昧さと明確な規則の両方をうまく使い分けることにより、非終端記号を少なくすることができ、能率的な文法となる。

1.6 例

本書は、C言語の基本的サブセットであるsampleCの完全なコンパイラを示すことを目的としている。このコンパイラのいろいろなモジュールが、各章の終り近くにある“例”の節に示されている。

ここに示す例は、拡張BNFで書かれたsampleCの非公式の定義である。ここでは特殊文字からなる終端記号を引用符(')でくくり、予約語は大文字で書かれている。終端記号IdentifierとConstantが付け加えられているが、これらは他と異なり、単語の代わりとはなるが、それ白身の代わりとはならない。この例における定義は、さらに改良して簡単にするという課題を後に出題できるように多少冗長になっている。

program
        : definition { definiton }

definition
        : data_definition
	| function_definition

data_definition
        : INT declarator { ',' declarator } ';'

declarator
        : Identifier

function_definition
        : [ INT ] function_header function_body

function_header
        : declarator paramter_list

parameter_list
        : '(' [ Identifier_list ] ')' { parameter_decalration }

Identifier_list
        : Identifier { ',' Identifier }

parameter_declaration
        : INT declarator { ',' declarator } ';'

funtion_body
        : '{' { data_definition } { statement } '}'

statement
        : [ expression ] ';'
	| '{' { data_definition } { statement } '}'
	| IF '(' expression ')' statement [ ELSE statement ]
	| WHILE '(' expression ')' statement
	| BREAK ';'
	| CONTINUE ';'
	| RETURN [ expression ] ';'

expression
        : binary { ',' binary }

binary
        : Identifier '=' binary                 from right
	| Identifier '+=' binary
	| Identifier '-=' binary
	| Identifier '*=' binary
	| Identifier '/=' binary
	| binary '==' binary    precedence      from left
	| binary '!=' binary
	| binary '<' binary     precedence
	| binary '<=' binary
	| binary '>' binary
	| binary '>=' binary
	| binary '+' binary     precedence
	| binary '-' binary
	| binary '*' binary     precedence
	| binary '/' binary
	| binary '%' binary
	| unary

unary
        : '++' Identifier
	| '--' Identifier
	| primary

primary
        : Identifier
	| Constant
	| '(' expression ')'
	| Identifier '(' [ argument_list ] ')'

argument_list
        : binary { ',' binary }

sampleCのセマンディックスは、多少省略されているが、基本的にCのセマンディックスと同じである。sampleCは、intのデータ・タイプ,可変のパラメータを受け取り、結果としてintを返す関数、スカラーの外部変数、関数あるいはブロックにおける局所スカーラー変数、およびif-elseとwhileの制御構造だけを持つ。また、多くのCの演算子が使えるようになっている。しかし、一時に一つのファイルしかコンパイルできず、また、必ずmain()の関数がなければならない。この最後の条件については、第5章において明確にする。

以上の非公式の定義がBNFに翻訳されている。ここでは再帰を用いた繰返し構造を用いている。また、%tokenの定義と優先順位の関係の記述が加えられている。以下の定義はyaccに対する正しい入力となる。

/*
 *	sample C
 *	syntax analysis
 *	(s/r conflict: one on ELSE)
 */

/*
 *	terminal symbols
 */

%token	Identifier
%token	Constant
%token	INT
%token	IF
%token	ELSE
%token	WHILE
%token	BREAK
%token	CONTINUE
%token	RETURN
%token	';'
%token	'('
%token	')'
%token	'{'
%token	'}'
%token	'+'
%token	'-'
%token	'*'
%token	'/'
%token	'%'
%token	'>'
%token	'<'
%token	GE	/* >= */
%token	LE	/* <= */
%token	EQ	/* == */
%token	NE	/* != */
%token	'&'
%token	'^'
%token	'|'
%token	'='
%token	PE	/* += */
%token	ME	/* -= */
%token	TE	/* *= */
%token	DE	/* /= */
%token	RE	/* %= */
%token	PP	/* ++ */
%token	MM	/* -- */
%token	','

/*
 *	precedentce table
 */

%right	'=' PE ME TE DE RE
%left	'|'
%left	'^'
%left	'&'
%left	EQ NE
%left	'<' '>' GE LE
%left	'+' '-'
%left	'*' '/' '%'
%right	PP MM

%%

program
	: definitions

definitions
	: definition
	| definitions definition

definition
	: function_definition
	| INT function_definition
	| declaration

function_definition
	: Identifier '(' optional_parameter_list ')'
	| parameter_declarations compound_statement

optional_parameter_list
	: /* no formal parameters */
	| parameter_list

parameter_list
	: Identifier
	| parameter_list ',' Identifier

parameter_declarations
	: /* null */
	| parameter_declarations parameter_declaration

parameter_declaration
	: INT parameter_declarator_list ';'

parameter_declarator_list
	: Identifier
	| parameter_declarator_list ',' Identifier

compound_statement
	: '{' declarations statements '}'

declarations
	: /* null */
	| declarations declaration

declaration
	: INT declarator_list ';'

declarator_list
	: Identifier
	| declarator_list ',' Identifier

statements
	: /* null */
	| statements statement

statement
	: expression ';'
	| ';'	/* null statement */
	| BREAK ';'
	| CONTINUE ';'
	| RETURN ';'
	| RETURN expression ';'
	| compound_statement
	| if_prefix statement
	| if_prefix statement ELSE statement
	| loop_prefix statement

if_prefix
	: IF '(' expression ')'

loop_prefix
	: WHILE '(' expression ')'

expression
	: binary
	| expression ',' binary

binary
	: Identifier
	| Constant
	| '(' expression ')'
	| Identifier '(' optional_argument_list ')'
	| PP Identifier
	| MM Identifier
	| binary '+' binary
	| binary '-' binary
	| binary '*' binary
	| binary '/' binary
	| binary '%' binary
	| binary '>' binary
	| binary '<' binary
	| binary GE binary
	| binary LE binary
	| binary EQ binary
	| binary NE binary
	| binary '&' binary
	| binary '^' binary
	| binary '|' binary
	| Identifier '=' binary
	| Identifier PE binary
	| Identifier ME binary
	| Identifier TE binary
	| Identifier DE binary
	| Identifier RE binary

optional_argument_list
	: /* no actual arguments */
	| argument_list

argument_list
	: binary
	| argument_list ',' binary

1.7 記述における注意

前に述べたように、yaccの入力はほとんどフリー・フォーマットであるが、ある種の取り決めを定めておく方が良い。たとえは、次のようなものである。

非終端記号は規則の左辺に一度だけ現われるようにする。ここでは1行に一つの非終端記号だけを左詰めにして記している。フォーミュレーションはすべてひとまとめにする。
規則の左辺と右辺の間のコロンは行の最初のタブ位置に置き、最初のフォーミュレーションはコロンの後にブランクを一つあけておく。アクション(第3章で述べる)は二つ目のタブ位置に置く。
コロン、次のフォーミュレーションをつなぐバー(1)、および規則を終了させるセミコロンは位置を合わせる。

はyaccにおいては問題ないが、コロンとバーの間違いなどが生じやすいので、セミコロンを省略するのは良くない。

規則と規則はブランク行で分ける。
空のフォーミュレーションは適当なコメントを付けてはっきりと区別する。これはデバッグの際に役に立つ。
この本では、長い名前を使う場合にはアンダースコアを用いるようにしている。ピリオドも同じ目的で使うことができる。また、カンマで区切られたいくつかのものや、一連のものを表わす場合は_listという文字列を後に付けるようにしている。

1.8 問題

Pasca1の小さなサブセットをデザインし、そのBNFの記述を書いてみよ。そして、

tokenの定義と優先順位の関係をそのBNFの記述に付け加えよ。BNFの記述がyaccの

入力として受け入れられるまで、すなわち、無視することのできるシフトとリデュースの重複以外のエラー・メッセージを出力しなくなるまで修正せよ。
sampleCの定義を、配列のようなC言語の他の標準の機能を加えて拡張せよ。そして、

新しいsampleCの記述がyaccに受け入れられるように、1.6節で与えられた文法を変更せよ。
拡張BNFの文法をBNFで書け。拡張BNFで書かれた拡張BNFの文法は1.2節に示されている。この文法をBNFに変更するには何が必要か? tokenの定義、および最終的に文法がyaCCに受け入れられるために必要なものを追加せよ。

ヒント:シフトとリデュースの重複をなくす目的で、規則を終了させるためにセミコロンを利用したくなるであろう。

Cコンパイラ設計(yacc・lexの応用)/言語の定義